РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ

КВАДРАТНОЕ УРАВНЕНИЕ - это уравнение вида

                 ,

где x - переменная, a,b,c - постоянные (числовые) коэффициенты.

В основном решение квадратных уравнений сводится к нахождению дискриминанта:  D=b²-4ac.

       О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :

• D>0 - уравнение имеет 2 различных вещественных корня
• D=0 - уравнение имеет 2 совпадающих вещественных корня
• D<0 - уравнение имеет 2 мнимых корня (для непродвинутых пользователей - корней не имеет)

В общем случае корни уравнения равны:

Очевидно, в случае с нулевым дискриминантом, оба корня равны

.

Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:

 

В таком случае корни уравнения вычисляются по формуле:

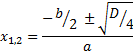
ТЕОРЕМА ВИЕТА.

Приведенным квадратным уравнением называется уравнение вида

,

то есть квадратное уравнение с единичным коэффициентом при старшем члене.

В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:

.

Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене, то есть при х².